Syntaxis:
We kunnen het voortschrijdend gemiddelde op verschillende manieren berekenen, namelijk:
Methode 1:
NumPy. cumsum ( )Het geeft de som van de elementen in de gegeven array terug. We kunnen het voortschrijdend gemiddelde berekenen door de uitvoer van cumsum() te delen door de grootte van de array.
Methode 2:
NumPy. en . gemiddeld ( )Het heeft de volgende parameters.
a: gegevens in matrixvorm die moeten worden gemiddeld.
axis: het gegevenstype is int en het is een optionele parameter.
gewicht: het is ook een array en een optionele parameter. Het kan dezelfde vorm hebben als een 1-D-vorm. In het geval van eendimensionaal moet het een gelijke lengte hebben als die van een 'a' -array.
Merk op dat er geen standaardfunctie in NumPy lijkt te zijn om het voortschrijdend gemiddelde te berekenen, dus het kan op een andere manier worden gedaan.
Methode 3:
Een andere methode die kan worden gebruikt om het voortschrijdend gemiddelde te berekenen is:
bijv. convolueren ( a , in , modus = 'vol' )In deze syntaxis is a de eerste invoerdimensie en v de tweede invoerdimensionale waarde. Mode is de optionele waarde, deze kan vol, hetzelfde en geldig zijn.
Voorbeeld # 01:
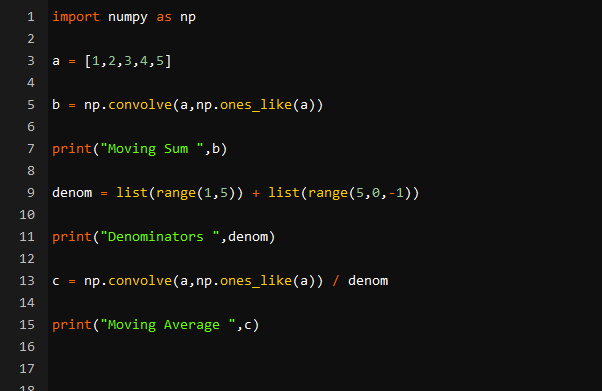
Laten we nu een voorbeeld geven om meer uit te leggen over het voortschrijdend gemiddelde in Numpy. In dit voorbeeld nemen we het voortschrijdend gemiddelde van een array met de convolve-functie van NumPy. We nemen dus een array 'a' met 1,2,3,4,5 als zijn elementen. Nu zullen we de functie np.convolve aanroepen en de uitvoer ervan opslaan in onze 'b' -variabele. Daarna zullen we de waarde van onze variabele 'b' afdrukken. Deze functie berekent de bewegende som van onze invoerarray. We zullen de uitvoer afdrukken om te zien of onze uitvoer correct is of niet.
Daarna zullen we onze output converteren naar het voortschrijdend gemiddelde met dezelfde convolve-methode. Om het voortschrijdend gemiddelde te berekenen, hoeven we alleen de voortschrijdende som te delen door het aantal steekproeven. Maar het grootste probleem hier is dat, aangezien dit een voortschrijdend gemiddelde is, het aantal monsters blijft veranderen, afhankelijk van de locatie waar we ons bevinden. Dus om dat probleem op te lossen, maken we gewoon een lijst met de noemers en moeten we dit omzetten in een gemiddelde.
Voor dat doel hebben we een andere variabele 'denom' voor de noemer geïnitialiseerd. Het is eenvoudig om de lijst te begrijpen met behulp van de bereiktruc. Onze array heeft vijf verschillende elementen, dus het aantal monsters op elke plaats gaat van één naar vijf en vervolgens terug van vijf naar één. We zullen dus gewoon twee lijsten bij elkaar optellen en ze opslaan in onze parameter 'denom'. Nu gaan we deze variabele afdrukken om te controleren of het systeem ons de ware noemers heeft gegeven of niet. Daarna zullen we onze bewegende som delen door de noemers en deze afdrukken door de uitvoer op te slaan in de variabele 'c'. Laten we onze code uitvoeren om de resultaten te controleren.
importeren numpy net zo bijv.a = [ 1 , twee , 3 , 4 , 5 ]
b = bijv. convolueren ( a , bijv. one_like ( a ) )
afdrukken ( 'Bewegende som' , b )
naam = lijst ( bereik ( 1 , 5 ) ) + lijst ( bereik ( 5 , 0 , - 1 ) )
afdrukken ( 'noemers' , naam )
c = bijv. convolueren ( a , bijv. one_like ( a ) ) / naam
afdrukken ( 'Bewegend gemiddelde' , c )
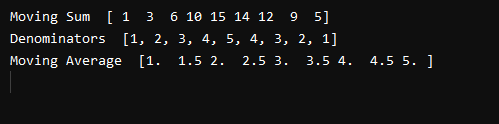
Na de succesvolle uitvoering van onze code, krijgen we de volgende uitvoer. In de eerste regel hebben we de “Moving Sum” afgedrukt. We kunnen zien dat we '1' aan het begin en '5' aan het einde van de array hebben, net zoals we hadden in onze originele array. De rest van de getallen zijn de sommen van verschillende elementen van onze array.
Zes op de derde index van de array komt bijvoorbeeld van het toevoegen van 1,2 en 3 van onze invoerarray. Tien op de vierde index komt van 1,2,3 en 4. Vijftien komt van het optellen van alle getallen, enzovoort. Nu, in de tweede regel van onze uitvoer, hebben we de noemers van onze array afgedrukt.
Uit onze uitvoer kunnen we zien dat alle noemers exact zijn, wat betekent dat we ze kunnen delen met onze bewegende somreeks. Ga nu naar de laatste regel van de uitvoer. In de laatste regel kunnen we zien dat het eerste element van onze Moving Average Array 1 is. Het gemiddelde van 1 is 1 dus ons eerste element is correct. Het gemiddelde van 1+2/2 wordt 1,5. We kunnen zien dat het tweede element van onze uitvoerarray 1.5 is, dus het tweede gemiddelde is ook correct. Het gemiddelde van 1,2,3 wordt 6/3=2. Het maakt ook onze output correct. Dus uit de uitvoer kunnen we zeggen dat we met succes het voortschrijdend gemiddelde van een array hebben berekend.
Conclusie
In deze gids hebben we geleerd over voortschrijdende gemiddelden: wat voortschrijdend gemiddelde is, wat het gebruikt en hoe het voortschrijdend gemiddelde te berekenen. We hebben het in detail bestudeerd vanuit zowel wiskundig als programmeerkundig oogpunt. In NumPy is er geen specifieke functie of proces om het voortschrijdend gemiddelde te berekenen. Maar er zijn verschillende andere functies waarmee we het voortschrijdend gemiddelde kunnen berekenen. We hebben een voorbeeld gemaakt om het voortschrijdend gemiddelde te berekenen en hebben elke stap van ons voorbeeld beschreven. Voortschrijdende gemiddelden zijn een handige manier om toekomstige resultaten te voorspellen met behulp van bestaande gegevens.