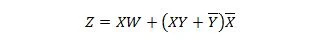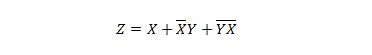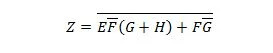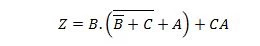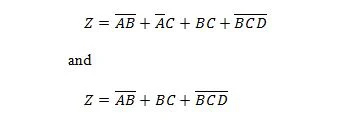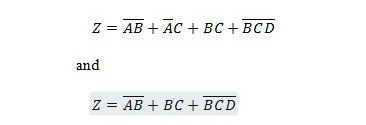Hoofdstuk 2: Booleaanse algebra en de bijbehorende computercomponenten

Hoofdstuk 2: Booleaanse algebra en de bijbehorende computercomponenten

2.1 Basis Booleaanse operatoren

Stel dat ik (de auteur) lang ben en jij (de lezer) lang bent. Als iemand je vraagt ​​of we allebei lang zijn, zeg je ‘Ja’ (waar). Als hij vraagt ​​of we allebei klein zijn, zou je “Nee” zeggen (onwaar). Als jij klein bent en ik lang, en hij vraagt ​​je of jij of ik lang is, dan zou je antwoord “Ja” (waar) zijn. Als hij vraagt ​​of jij en ik lang zijn, zou je geen antwoord hebben. Je zou verder kunnen zeggen dat de laatste vraag niet gesteld mag worden of dat er geen antwoord op de vraag bestaat. Welnu, ik wil dat u (de lezer) weet dat deze vraag vandaag de dag, onder bepaalde omstandigheden, gesteld moet worden.

In de biologie is een persoon lang of klein. Het zijn de ‘omgevings’-omstandigheden die ervoor zorgen dat iemand een gemiddelde lengte heeft. Eén wetenschapper, George Boole, definieerde een reeks antwoorden of regels voor dit soort vragen. Deze regels leren we in dit gedeelte van de online loopbaancursus (hoofdstuk). Deze regels worden tegenwoordig gebruikt in computers, programmeren, elektronica en telecommunicatie. Zonder deze regels zou je feitelijk geen computer hebben, zoals dat tegenwoordig gebruikelijk is; je zou niet ook programmeren hebben, zoals tegenwoordig gebruikelijk is.

Waar of niet waar
Een eenvoudige uitspraak in menselijke taal is op zichzelf waar of onwaar. Als ik zeg: ‘Ik ben lang’, is dat waar of niet waar. Als ik zeg: ‘Je bent lang’, is dat waar of niet waar. Als ik lang ben en jij klein, en de vraag wordt gesteld of zowel jij als ik lang zijn, moet in de Booleaanse logica een antwoord met waar of onwaar worden gegeven. Welke van deze twee moet worden gegeven? Boole heeft deze vraag niet echt beantwoord. Hij heeft eenvoudigweg een aantal regels bedacht die we moeten volgen. Het goede nieuws is dat als je deze regels in de juiste context volgt, er geen onduidelijkheid meer is. Dankzij deze regels hebben we tegenwoordig computers en programmering. De regels worden u nu gegeven. De regels kunnen niet echt worden uitgelegd; je accepteert ze gewoon. De regels staan ​​onder drie kopjes: AND, OR en NOT.

EN
De vraag kan gesteld worden of zowel jij als ik lang zijn. Mijn lengte en jouw lengte worden vervolgens gecombineerd door de EN-set regels. Dit zijn de AND-regels die u moet volgen:

onwaar EN onwaar = onwaar
onwaar EN waar = onwaar
waar EN onwaar = onwaar
waar EN waar = waar

Laat nu lang waar zijn en kort onwaar. Dit betekent dat als ik klein ben EN jij klein bent, jij en ik ook klein zijn. Als ik klein ben EN jij lang bent, zijn jij en ik klein; dat is het Booleaanse antwoord dat u moet accepteren. Als ik lang ben EN jij klein bent, zijn zowel jij als ik klein. Als ik lang ben EN jij bent lang, dan zijn jij en ik ook lang. Dit zijn allemaal EN Booleaanse regels die u (de lezer) gewoon hoeft te accepteren.

OF
De vraag kan gesteld worden of jij OF ik lang is. Mijn lengte en jouw lengte worden vervolgens gecombineerd door de OR-regels. Dit zijn de OR-regels die u moet volgen:

onwaar OF onwaar = onwaar
onwaar OF waar = waar
waar OF onwaar = waar
waar OF waar = waar

Nogmaals, laat lang waar zijn en kort vals. Dit betekent dat als ik tekortschiet OF jij tekortschiet, jij OF ik tekortschiet. Als ik klein ben OF jij lang bent, ben jij of ik lang. Als ik lang ben OF jij klein bent, ben jij OF ik lang. Als ik lang ben OF jij bent lang, dan ben jij of ik lang. Dit zijn allemaal Booleaanse regels die u moet accepteren.

NIET
Nu bestaan ​​er in de Booleaanse logica slechts twee toestanden (mogelijke antwoorden). Dat wil zeggen: als je NIET lang bent, ben je klein. Als je NIET klein bent, ben je lang; niks anders. Dit zijn de NIET-regels die u moet volgen:

NIET onwaar = waar
NIET waar = onwaar

Stel dat je een touwtje (of veer) hebt dat je kunt uittrekken (trekken). Terwijl de snaar zich in zijn natuurlijke staat bevindt, zou je hem verlengen als ik zeg: 'NIET kort',; dat is de interpretatie. Terwijl de snaar wordt verlengd, als ik zeg: 'NIET lang', zou je hem laten samentrekken; dat is de interpretatie.

Je moet alle gegeven regels in hun verschillende categorieën onthouden.

Meer dan twee operanden
In een computertaal worden AND, OR en NOT elk een operator genoemd. Voor de NOT-operator heeft u slechts één operand (waarde voor een operator) nodig om een ​​antwoord te krijgen. Voor de AND- of OR-operatoren kunt u meer dan twee operanden hebben. In de voorgaande gevallen zijn twee operanden voor AND en OR weergegeven. U kunt als volgt drie operanden voor AND hebben:

onwaar EN onwaar EN onwaar = onwaar
onwaar EN onwaar EN waar = onwaar

Dit zijn twee lijnen; elk heeft twee EN-operatoren. Er zijn eigenlijk negen regels als de operanden drie zijn. Met de AND-operator is alleen de laatste regel (negende regel) gelijk aan waar; alle voorgaande regels zijn onwaar. Merk op dat met twee operanden voor AND alleen de laatste regel nog waar is; alle voorgaande drie regels zijn onwaar. Als er vier operanden zijn, zijn er zestien regels en geldt alleen de laatste regel voor de AND-operator.

Het patroon voor AND en het patroon voor OR zijn verschillend. Met drie operanden voor twee OR-operatoren zijn er ook negen regels en deze keer is alleen de eerste regel onwaar. De tweede tot en met de negende regel zijn waar. Merk op dat met twee operanden voor OR alleen de eerste regel nog waar is; alle overige drie regels zijn onwaar. Als de operanden vier zijn voor OR, zijn er ook 16 lijnen.

De NOT-operator behandelt slechts één operand. Het NIET onwaar is waar en het NIET waar is onwaar.

2.2 Twee operand-waarheidstafels en hun elektronische componenten

In de wiskunde bestaat er een onderwerp dat algebra heet. Een klein deel ervan is in het vorige hoofdstuk gezien. Er bestaat een soort algebra die Booleaanse algebra wordt genoemd. In de Booleaanse algebra wordt waar geïdentificeerd door het grondtal twee, dat 1 is, en onwaar wordt geïdentificeerd door het grondtal twee, dat 0 is.

De componenten van de interne computereenheid zijn elektronische componenten. De systeemeenheid van het computersysteem bestaat uit digitale elektronische componenten. De AND-bewerking wordt uitgevoerd door een klein elektronisch onderdeel dat de AND-poort wordt genoemd. De OF-bewerking wordt uitgevoerd door het kleine elektronische onderdeel dat de OF-poort wordt genoemd. De NOT-bewerking wordt uitgevoerd door het kleine elektronische onderdeel dat de NOT-poort wordt genoemd. Te veel van deze poorten kunnen zich in een Integrated Circuit (IC)-chip bevinden.

EN Waarheidstafel en zijn poort
De volgende tabel geeft de AND-waarheidstabel en het AND-poortsymbool (klein circuit):

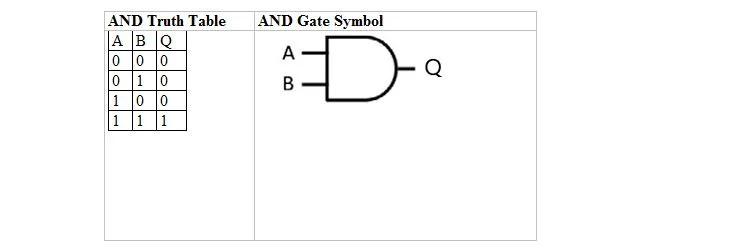
Voor zowel de AND-waarheidstabel als de poort ervan zijn zowel A als B twee invoervariabelen. Q is de uitvoervariabele. A is 1 of 0. B is 1 of 0. Q is 1 of 0. De EN-waarheidstabel met 1-en en 0-en is hetzelfde als de vorige waar/onwaar-EN-waarheidsindeling (tabel). De EN-vergelijking is:

A . B = Q

waarbij de punt (.) AND (Boolean) betekent. De punt kan worden weggelaten om AB = Q te hebben, wat hetzelfde betekent (EN).

Opmerking: De bits voor A en B in de vier rijen, als paren, zijn de eerste vier getallen in basis twee, beginnend bij 0 (of 00), d.w.z. 00, 01, 10, 11.

De volgende tabel geeft de OF-waarheidstabel en het OF-poortsymbool (klein circuit):

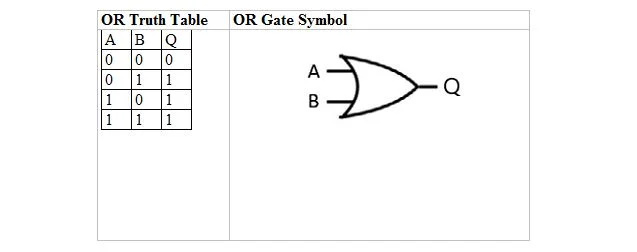
Voor zowel de OR-waarheidstabel als de poort ervan zijn zowel A als B twee invoervariabelen. Q is de uitvoervariabele. De OR-waarheidstabel met 1-en en 0-en is hetzelfde als de vorige waar/onwaar-OR-waarheidsindeling (tabel).

De OR-vergelijking is:

A + B = Q

Waar de + hier Booleaanse OR betekent en niet optelling. De vergelijking wordt gelezen als “A of B is gelijk aan Q”.

De volgende tabel geeft de NOT-waarheidstabel en het NOT-poortsymbool (klein circuit):

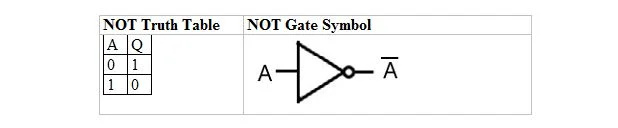
De NOT-waarheidstabel of NOT-poort heeft slechts één ingang en één uitgang. Als de invoer 0 is, is de uitvoer 1. Als de invoer 1 is, is de uitvoer 0. De NOT-poort voert een soort inversie uit. De uitvoervariabele is hetzelfde als de invoervariabele, maar met een balk (omlijnd). De NIET-waarheidstabel met 1-en en 0-en is hetzelfde als de vorige waar/onwaar-OR-waarheidsindeling (tabel).

De NIET-vergelijking is:

EEN = Q

Waar Q = A en de balk boven A hier complement betekent. Het complement van 0 is 1 en het complement van 1 is 0. De NOT-poort wordt ook wel de INVERTING-poort genoemd.

Dit zijn de fundamentele (of root) waarheidstabellen en hun poorten (kleine circuits) in digitale elektronica (met Booleaanse algebra). De andere drie waarheidstabellen die in de volgende illustratie worden gegeven en hun poorten zijn gemakshalve bedoeld en zijn gebaseerd op de voorgaande drie waarheidstabellen.

Er is een waarheidstabel en -poort die zijn afgeleid van de EN-waarheidstabel en -poort. Ze worden de NAND-waarheidstabel (voor NIET EN) en de bijbehorende NAND-poort genoemd. De NAND-waarheidstabel en zijn NAND-poort zijn:

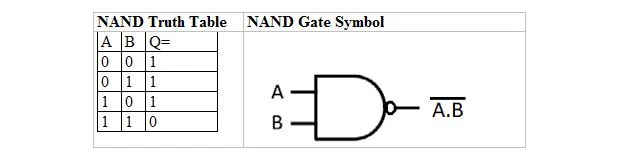
Om de NAND-waarheidstabel te verkrijgen, gaat u naar de uitvoer van de EN-waarheidstabel en vervangt u elk cijfer door zijn complement. Het complement van 0 is 1 en het complement van 1 is 0. De NAND-poort lijkt op de EN-poort, maar heeft een kleine cirkel vóór de uitgangslijn. De NAND-vergelijking is:

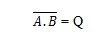
Waar betekent het complement van het resultaat van “A” EN “B”. De balk (bovenlijn) wordt in de poort weergegeven door de kleine cirkel. Merk op dat de punt tussen A en B kan worden weggelaten.

Er is nog een waarheidstabel en -poort die zijn afgeleid van de OR-waarheidstabel en -poort. Ze worden de NOR-waarheidstabel (voor NOT OR) en de bijbehorende NOR-poort genoemd. De NOR-waarheidstabel en zijn NOR-poort zijn:

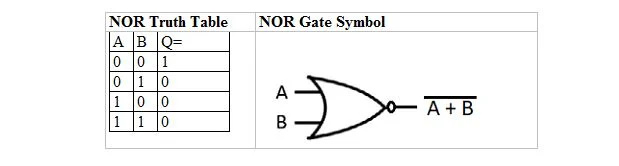
Om de NOR-waarheidstabel te verkrijgen, gaat u naar de uitvoer van de OF-waarheidstabel en vervangt u elk cijfer door zijn complement. Het complement van 0 is 1 en het complement van 1 is 0. De NOR-poort lijkt op de OF-poort, maar heeft een kleine cirkel vóór de uitgangslijn. De NOR-vergelijking is:

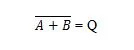
Waar 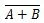betekent het complement van het resultaat van “A” OF “B”. De balk (bovenlijn) wordt in de poort weergegeven door de kleine cirkel.

Exclusief OF (XOR)
De waarheidstabel voor de OF-poort is:

In normaal Engels is het niet duidelijk of de laatste rij van 1 OR 1 1 of 0 moet opleveren. In de Booleaanse algebra zijn er dus twee soorten OR-waarheidstabellen en twee overeenkomstige poorten. Bij de normale OR geeft de laatste rij van 1 OR 1 1. Het andere type OR is de exclusieve OR (XOR) waarbij de eerste drie rijen hetzelfde zijn als de eerste drie rijen van normale OR (inclusief uitvoer). Voor de vierde en laatste rij geeft 1 OF 1 echter 0.

De volgende tabel geeft de XOR-waarheidstabel en het XOR-poortsymbool (klein circuit):

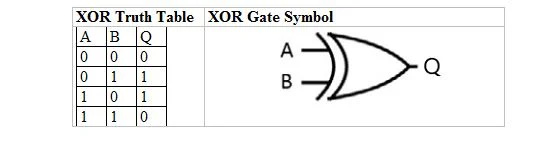
Voor zowel de XOR-waarheidstabel als de poort ervan zijn zowel “A” als “B” twee invoervariabelen. “Q” is de uitvoervariabele.

De XOR-vergelijking is:

EEN ⊕ B = Q

Waar de ⊕ hier Booleaanse XOR betekent.

De normale OR betekent een van beide of beide. Exclusief OR betekent strikt of en niet allebei.

2.3 Booleaanse postulaten

Postulaten zijn aannames op basis waarvan bepaalde conclusies worden getrokken. Er zijn tien Booleaanse postulaten die hun oorsprong vinden in de AND-, OR- en NOT-vergelijkingen (waarheidstabellen). Deze vergelijkingen worden ook wel functies genoemd. De fundamentele functies worden als volgt herhaald:

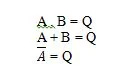
Dit zijn de fundamentele functies (vergelijkingen) in de Booleaanse algebra. De volgende andere drie (functie)vergelijkingen zijn geen fundamentele functies:

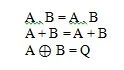
Hoewel de laatste functie hier bijzonder is, wordt deze niet als een fundamentele functie beschouwd.

De Booleaanse postulaten zijn als volgt:

Van AND-functie
1) 0 . 0 = 0
twintig. 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1

Van OF-functie
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1

Van NIET-functie
9) 0 = 1
10) 1 = 0

Opmerking: Deze postulaten zijn slechts de regels in de AND-, OR- en NOT-waarheidstabellen die op een onafhankelijke manier worden uitgedrukt. De lezer moet de gegeven postulaten uit het hoofd leren.

2.4 Booleaanse eigenschappen

Een eigenschap is een soort kenmerk van iets. Booleaanse eigenschappen zijn vergelijkingen die zijn afgeleid van de Booleaanse postulaten. In deze sectie worden de eigenschappen eenvoudigweg gegeven zonder hun afleidingen en daarna gebruikt. Er zijn vijfentwintig eigenschappen die als volgt onder tien rubrieken zijn gegroepeerd:

Eigenschappen van de AND-functie

Eigenschap 1:

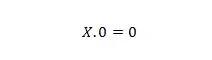
Waar X 1 of 0 kan zijn. Dit betekent dat, ongeacht wat X is, het resultaat altijd 0 is.

Opmerking: een variabele hoeft niet noodzakelijkerwijs A of B of C of D te zijn. Een variabele kan W of X of Y of Z of een andere letter zijn.

Eigenschap 2:

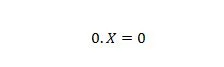
Waar X 1 of 0 kan zijn. Merk op dat het verschil tussen eigenschap 1 en eigenschap 2 is dat aan de linkerkant van het gelijkteken van beide vergelijkingen de posities van X en 0 zijn verwisseld.

Eigenschap 3:

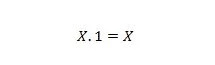
Als X 0 is, dan 0. 1 = 0. Als X 1 is, dan 1. 1 = 1.

Eigenschap 4:

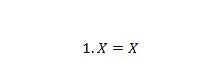
Als X 0 is, dan 1. 0 = 0. Als X 1 is, dan 1. 1 = 1. Merk op dat het verschil tussen eigenschap 3 en eigenschap 4 is dat aan de linkerkant van beide vergelijkingen de posities van X en 1 zijn verwisseld.

Eigenschappen van de OR-functie

Eigenschap 5:

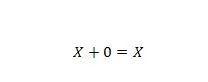
Waarbij X 1 of 0 kan zijn. Dit betekent dat als X 0 is, het resultaat 0 is. Als X 1 is, is het resultaat 1.

Eigenschap 6:

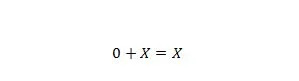
Waar X 1 of 0 kan zijn. Merk op dat het verschil tussen eigenschap 5 en eigenschap 6 is dat aan de linkerkant van beide vergelijkingen de posities van X en 0 zijn verwisseld.

Eigenschap 7:

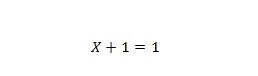
Als X 0 is, dan is 0 + 1 = 1. Als X 1 is, dan is 1 + 1 = 1.

Eigenschap 8:

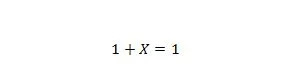
Als X 0 is, dan is 1 + 0 = 1. Als X 1 is, dan is 1 + 1 = 1. Merk op dat het verschil tussen eigenschap 7 en eigenschap 8 is dat aan de linkerkant van beide vergelijkingen de posities van X en 1 zijn verwisseld.

Eigenschappen met betrekking tot de combinatie van een variabele met zichzelf of zijn complement

Eigenschap 9:

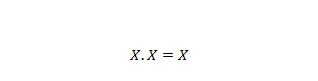
Dat wil zeggen: als X 0 is, dan 0 . 0 = 0. Als X 1 is, dan 1 . 1 = 1.

Eigenschap 10:

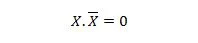
Dat wil zeggen: als X 0 is, dan 0. 1 = 0. Als X 1 is, dan 1. 0 = 0.

Voor opeenvolgende variabelen wordt deze eigenschap:

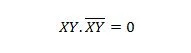
Eigenschap 11:

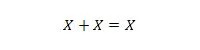
Dat wil zeggen: als X 0 is, dan 0 + 0 = 0. Ials X 1 is, dan 1 + 1 = 1 (van normale OR).

Eigenschap 12:

Dat wil zeggen: als X 0 is, dan 0 + 1 = 1. Als X = 1, dan 1 + 0 = 1.

Dat wil zeggen: als X 0 is, dan 0 + 1 = 1. Als X = 1, dan 1 + 0 = 1.

Dubbele aanvulling

Eigenschap 13:

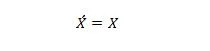
Als X aan de linkerkant 0 is, wordt X aan de rechterkant 0. Als X aan de rechterkant 1 is, wordt X aan de linkerkant 1. Met andere woorden: dubbele complementen geven de oorspronkelijke waarde terug.

Commutatieve wet

Eigenschap 14:

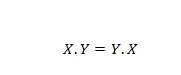
Dit betekent dat het verwisselen van de eerste en de tweede operanden voor de AND-operator, aan de linkerkant van het gelijkteken, er niet toe doet; het antwoord is nog steeds hetzelfde nadat de uitwisseling aan de linkerkant heeft plaatsgevonden. Deze vergelijking kan worden geschreven zonder de punten weg te laten als: XY = YX.

Eigenschap 15:

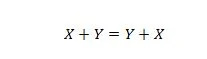
De uitleg hier is dezelfde als in de vorige AND, maar dan voor de OR-operator.

Distributief recht

Eigenschap 16:

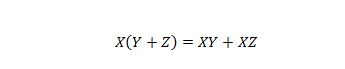
Hier zijn er drie variabelen: X, Y en Z. Elke variabele kan 1 of 0 zijn. Aan de linkerkant van het gelijksymbool betekenen de haakjes dat eerst moet worden geëvalueerd wat erin zit. Dan is AND het resultaat met X. Het rechterlid zegt dat de X EN Y samen, OF de X EN Z samen, hetzelfde zijn als het linkerlid. Merk op dat de puntoperator voor de AND's geheel wordt weggelaten; en de samengevoegde variabelen betekenen nog steeds AND.

Eigenschap 17:

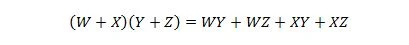
Deze eigenschap is een uitbreiding van eigenschap 16 met de toegevoegde variabele W.

Associatief recht

Eigenschap 18:

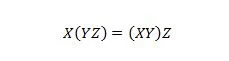
Met haakjes bedoelen we eerst evalueren wat er tussen haakjes staat. Dus, voor de uitdrukking aan de linkerkant: als Y met Z eerst een AND-bewerking krijgen, en X een AND-bewerking krijgt met het resultaat, dan is dat eindresultaat aan de linkerkant hetzelfde als het eindresultaat aan de rechterkant -zijde waar X met Y eerst met AND wordt bewerkt voordat het resultaat met Z wordt geAND. Merk op dat de punten in de vergelijking zijn weggelaten.

Eigenschap 19:

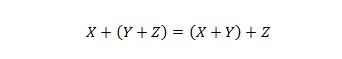
Deze eigenschap wordt op dezelfde manier uitgelegd als eigenschap 18, maar er wordt gebruik gemaakt van de OR-operator in plaats van de AND-operator. De OR-operator + wordt omwille van de eenvoud nooit weggelaten uit een Booleaanse expressie. Aan de andere kant kan de AND-operator worden weggelaten en kunnen de twee variabelen worden samengevoegd.

Absorptie

Eigenschap 20:

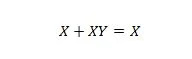
Met deze vergelijking zal, ongeacht wat Y is, de rechterkant altijd X zijn (geabsorbeerd).

Eigenschap 21:

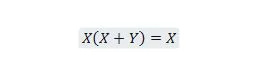
Bovendien zal met deze vergelijking, ongeacht wat Y is, de rechterkant altijd X zijn (geabsorbeerd). Deze eigenschap 21 is hetzelfde als eigenschap 20, namelijk:

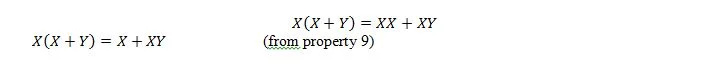
Hier gebruiken we de distributieve wet en het feit dat X.X = X van eigenschap 9.

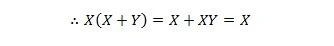
Een identiteit

Eigenschap 22:

Dit betekent dat voor de X + Y-uitdrukking het complement van X vóór Y de uitdrukking niet verandert.

Eigenschap 23:

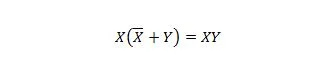
Dit betekent dat voor de XY-expressie het complement van X ORed met Y tussen haakjes, wat als eerste wordt gedaan, de XY-expressie niet verandert.

De wet van DeMorgan

Eigenschap 24:

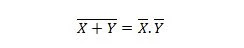
Dit betekent dat een NOR-poort (NOT OR) hetzelfde resultaat heeft als het NOTen van de twee ingangen voordat ze AND worden.

Eigenschap 25:

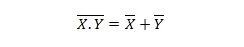
Dit betekent dat een NAND-poort (NOT AND) hetzelfde resultaat heeft als het NOTen van de twee ingangen vóór OR-ing.

De meegeleverde illustraties zijn de 25 eigendommen. Ze kunnen worden bewezen door alle verschillende mogelijke waarden van 1-en en 0-en in elke uitdrukking aan de linkerkant te vervangen, om te zien of de uitdrukking (of het resultaat) aan de rechterkant wordt verkregen. De bewijzen worden als oefening voor de lezer achtergelaten.

2.5 Vereenvoudiging van samengestelde uitdrukkingen

De volgende twee functies zijn hetzelfde:

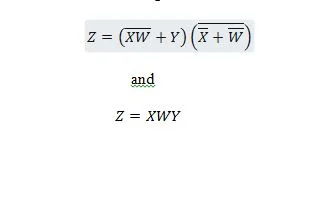
Z is de uitvoer en X, W en Y zijn de invoer. De eerste heeft een NAND-poort, een OF-poort, een EN-poort, twee NIET-poorten, een OF-poort en een NOR-poort nodig. De tweede heeft slechts twee EN-poorten nodig. De eerste is een vergelijking met een samengestelde uitdrukking aan de rechterkant, die is vereenvoudigd (gereduceerd) tot de enkele term voor de rechter uitdrukking voor de tweede vergelijking.

Vereenvoudiging of reductie leidt tot een kleiner aantal poorten om dezelfde functie als een circuit te implementeren. Zo'n kleiner circuit kan deel uitmaken van een geïntegreerd circuit (IC) of een op zichzelf staand circuit op het oppervlak van het moederbord van de computer.

Wanneer een functie (vergelijking) in het ontwerpproces arriveert, moet er vereenvoudiging plaatsvinden om het aantal poorten te verminderen en te eindigen met een goedkoper circuit. Vereenvoudiging vereist het gebruik van een of meer van de voorgaande vijfentwintig Booleaanse eigenschappen.

Voorbeeld 2.51:

Reduceer de vergelijking:

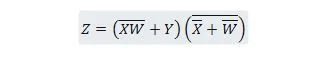
Opmerking: Twee haakjes naast elkaar betekent dat de haakjes een EN-teken hebben (de punt ertussen is optioneel niet geschreven).

Oplossing:
Bij de oplossingen staat rechts van de stap tussen haakjes de verantwoording (reden) van elke stap. De lezer moet elke stap en de rechtvaardiging ervan lezen. De lezer moet ook naar de voorgaande eigenschappen verwijzen als hij/zij de stappen voor functiereductie leest.

Voorbeeld 2.52:

Makkelijker maken:

2.6 Minimumbedrag aan producten

De volgende twee functies zijn hetzelfde:

Van beide rechteruitdrukkingen van beide vergelijkingen wordt gezegd dat ze de vorm van de som van producten (SP) hebben. Er wordt gezegd dat een uitdrukkelijke uitdrukking de vorm Som van Product heeft als deze geen haakjes bevat. Het is duidelijk dat de eerste functie (vergelijking) meer poorten nodig heeft dan de tweede functie.

De eerste rechteruitdrukking kan nog steeds worden gereduceerd om de tweede functie te verkrijgen. De tweede uitdrukking aan de rechterkant kan niet verder worden vereenvoudigd en nog steeds worden uitgedrukt als de som van producten (“optelling” van termen). De tweede uitdrukking aan de rechterkant kan eigenlijk niet verder worden vereenvoudigd. Er wordt dus gezegd dat het de vorm van de Minimum Sum of Products (MSP) heeft.

Voorbeeld 2.61:
Breng de volgende functie eerst naar het formulier Som van producten en vervolgens naar het formulier Minimumsom van producten.

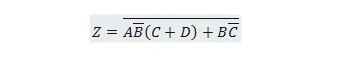
Oplossing:
Bij het oplossen van dit soort problemen moeten een of meer van de voorgaande vijfentwintig eigenschappen worden gebruikt, zoals geïllustreerd in deze oplossing:

2.6 Minimumbedrag aan producten

De volgende twee functies zijn hetzelfde:

Van beide rechteruitdrukkingen van beide vergelijkingen wordt gezegd dat ze de vorm van de som van producten (SP) hebben. Er wordt gezegd dat een uitdrukkelijke uitdrukking de vorm Som van Product heeft als deze geen haakjes bevat. Het is duidelijk dat de eerste functie (vergelijking) meer poorten nodig heeft dan de tweede functie.

De eerste rechteruitdrukking kan nog steeds worden gereduceerd om de tweede functie te verkrijgen. De tweede uitdrukking aan de rechterkant kan niet verder worden vereenvoudigd en nog steeds worden uitgedrukt als de som van producten (“optelling” van termen). De tweede uitdrukking aan de rechterkant kan eigenlijk niet verder worden vereenvoudigd. Er wordt dus gezegd dat het de vorm van de Minimum Sum of Products (MSP) heeft.

Voorbeeld 2.61:
Breng de volgende functie eerst naar het formulier Som van producten en vervolgens naar het formulier Minimumsom van producten.

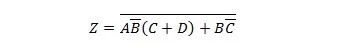
Oplossing:
Bij het oplossen van dit soort problemen moeten een of meer van de voorgaande vijfentwintig eigenschappen worden gebruikt, zoals geïllustreerd in deze oplossing:

Deze laatste uitdrukking heeft de vorm van de som van producten (SP), maar niet de vorm van de minimale som van producten (MSP). Het eerste deel van de vraag is beantwoord. De oplossing voor het tweede deel is als volgt:

Deze laatste vereenvoudigde functie (vergelijking) heeft de MSP-vorm en heeft voor implementatie minder poorten nodig dan de overeenkomstige SP-vorm. Onthoud: SP betekent Som van Producten, terwijl MSP Minimum Som van Producten betekent.

Voorbeeld 2.62:
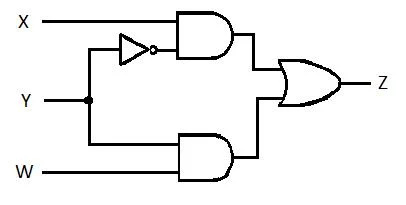
Het volgende circuit heeft de X-, Y- en W-ingangen en Z is de uitgang. Produceer de functie Som van Producten (SP) (schijnbare minimale som van producten) voor Z. Produceer vervolgens de werkelijke, meer gereduceerde (geminimaliseerde) Som van Producten (MSP). Implementeer vervolgens het MSP-circuit (teken het MSP-poortnetwerk).

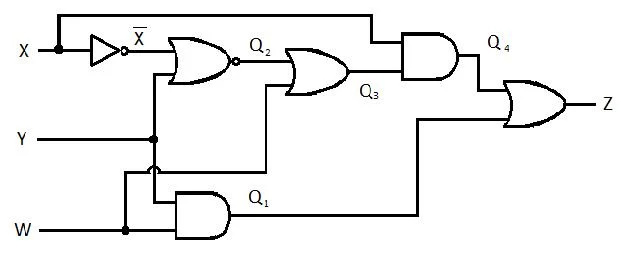
Afb. 2.61 Een poortcircuit

Oplossing:
Voordat het vereenvoudigingsproces begint, moet de uitdrukking voor Z worden verkregen in termen van X, Y en W. Raadpleeg deze voorbeeldillustratie uit het diagram:

Dit is de uitdrukking van Z in termen van X, Y en W. Hierna kan de vereenvoudiging naar schijnbare MSP plaatsvinden. Schijnbare MSP is SP.

Deze laatste vergelijking (functie) is in SP-vorm. Het is niet waar Minimale som van producten (nog geen MSP). De reductie (minimalisatie) moet dus doorgaan.

Deze laatste vergelijking (functie) is een echte Minimum Sum of Products (MSP). En het poortcircuit voor de minimale som van producten (echte minimalisatie) is:

Afb. 2.62 MSP-gatingcircuit

Opmerking
Uit de analyse in deze sectie blijkt dat het niet duidelijk is of de Som van Producten de Minimum Som van Producten is of niet. SP is niet erg nuttig. Het is MSP dat erg nuttig is. Er is een zekere manier om MSP te verkrijgen; het is om de Karnaugh-kaart te gebruiken. Karnaugh Map valt buiten het bestek van deze online carrièrecursus.

2.7 Problemen

De lezer wordt geadviseerd alle problemen in een hoofdstuk op te lossen voordat hij naar het volgende hoofdstuk gaat.

1. Produceer de AND-, OR- en NOT-waarheidstabellen met hun bijbehorende poorten.
2. Schrijf de tien Booleaanse postulaten op in hun verschillende categorieën, en noem de categorieën.
3. Schrijf zonder uitleg de zesentwintig eigenschappen van de Booleaanse algebra op in hun verschillende categorieën, en geef de categorieën een naam.
4. Reduceer de vergelijking met behulp van de Booleaanse eigenschappen en citeer de gebruikte categorieën.



5. Reduceer de vergelijking met behulp van de Booleaanse eigenschappen en citeer de gebruikte categorieën.



6. Gebruik de Booleaanse eigenschappen en citeer de gebruikte categorieën om de volgende vergelijking te reduceren – eerst naar Som van producten en vervolgens naar Minimum som van producten:



7. Gebruik de Booleaanse eigenschappen en citeer de gebruikte categorieën om de volgende vergelijking te reduceren – eerst naar Som van producten en vervolgens naar Minimum som van producten: