Hoofdstuk 3: Binaire getalbewerkingen in de microprocessor
3.1 Inleiding
In een computer worden rekenkundige bewerkingen uitgevoerd in 8 bits, 16 bits, 32 bits of 64 bits. Een getal als 3 in binair getal is 11. Als de bewerking in 8 bits moet worden uitgevoerd, wordt dit beschouwd als 00000011; ervoor met 0 nullen.
Voor een binair getal als 10000101 is het meest significante bit het bit uiterst links. In dit geval is dat 1. Het minst significante bit is het extreme bit aan de rechterkant, dat nog steeds 1 is, voor het getal. Het meest significante bit wordt afgekort als MSB. Het minst significante bit wordt afgekort als LSB.
De BInary digiT wordt afgekort als BIT en wordt eenvoudigweg geschreven als bit. In het getal 10010011 is elke één of nul een bit. Een groep van vier bits wordt een nibble genoemd. Een groep van acht bits wordt een byte genoemd. Een byte bestaat uit twee nibbles. De lagere knabbel is de knabbel voor de LSB en de hogere knabbel is de knabbel voor de MSB.
Een groep van 8 bits, 16 bits, 32 bits of 64 bits wordt een woord genoemd, zolang die groep informatie overbrengt die verder gaat dan alleen het aangeven van een getal. De groep wordt bijvoorbeeld een woord genoemd als het een instructie op laag niveau in de computer is. Er is ook een woord van 24 bits, maar dat wordt tegenwoordig niet vaak gebruikt.
Endianness verwijst naar de volgorde waarin de bytes een woord vormen. Beschouw het 24-bits woord – 100100001111010100100010. Dit woord bestaat uit drie bytes, namelijk:
10010000 11110101 00100010
De meest significante byte is de meest linkse byte. Wanneer de byte uiterst links de meest significante byte is en de byte uiterst rechts de minst significante byte, wordt dit de Big Endian-representatie van het woord genoemd. De Little Endian-weergave is het tegenovergestelde.
Het computergeheugen bestaat uit een reeks cellen en elke cel bevat een byte. De eerste cel in het computergeheugen is voor byte 0, de tweede voor byte 1, de derde voor byte 2, enzovoort. Bij big endianness en voor het vorige woord wordt de meest significante byte opgeslagen in byte 0-cel, de middelste byte in byte 1-cel en de minst significante byte in byte 2-cel. Dit betekent dat er meer significante bytes in de onderste geheugencel zitten.
Het vorige 24-bits woord kan als volgt in omgekeerde volgorde van bytes worden geschreven:
00100010 11110101 10010000
Nu bevindt de minst significante byte zich uiterst links en de meest significante byte uiterst rechts. Wanneer de byte uiterst links de minst significante byte is en de byte uiterst rechts de meest significante byte, is dit de Little Endian-representatie van het woord. Met weinig endianness en voor het vorige woord wordt de minst significante byte opgeslagen in byte 0-cel, de middelste byte wordt opgeslagen in byte 1-cel en de meest significante byte wordt opgeslagen in byte 2-cel. Dit betekent dat er minder significante bytes in de lagere geheugencel zijn.
Endianness wordt niet gebruikt voor bits in een byte. Het wordt ook niet gebruikt voor hapjes in een byte. Het wordt alleen gebruikt voor de bytevolgorde.
De getallenlijn
Een getal zonder teken is een positief getal. Positieve getallen zijn getallen vanaf nul naar boven. Er bestaan ook negatieve getallen. Positieve en negatieve getallen kunnen op een getallenlijn worden weergegeven. De volgende getallenlijn toont de positieve en negatieve gehele getallen (gehele getallen) nabij nul:
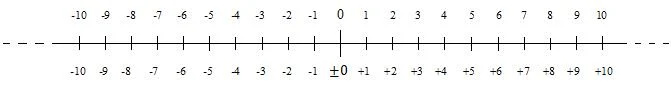
Negatieve getallen nemen af van nul naar beneden (naar links). In veel situaties wordt nul als positief beschouwd. In sommige situaties wordt het echter als negatief beschouwd. Daarom staat er in de lagere nummering in het diagram een plus- en minteken voor nul. Als een getal positief is, kan het teken ervan worden weggelaten; dit is het geval voor de bovenste nummering in het diagram. Het minteken voor een negatief getal wordt nooit weggelaten.
3.2 Optelling van binaire getallen
In de aanvulling:
A + B = S
A wordt de augend genoemd, B wordt de addend genoemd en S wordt de som genoemd.
Beschouw de volgende toevoeging van twee positieve getallen in grondtal twee:

In grondtal twee zijn de enige mogelijke cijfers 0 en 1. Optelling in grondtal 2 is vergelijkbaar met optelling in grondtal tien, maar twee in grondtal twee is één-nul (10). Wanneer de som van twee bits in een kolom 10 is, wordt 0 geschreven en wordt 1 naar de onmiddellijk linkerkolom overgebracht; opgeteld worden bij de som van de twee bits daar. Als de totale som drie is, betekent dit 11 in basis twee. De rechter 1 op 11 wordt geschreven en de linker 1 wordt meegenomen om te worden opgeteld bij de som van de onmiddellijke linkerkolombits. In beide gevallen wordt de 1 die naar links wordt gedragen de carry genoemd.
Als u de vorige opteltabel van rechts leest, is er in de tweede kolom (van rechts) een carry die het resultaat is van 1+1 = 10. In de derde kolom is er een carry die het resultaat is van 1+1+ carry van 1 = 11. In de vierde kolom is er een carry die het resultaat is van 0+1+ carry van 1 = 10. In de vijfde kolom is er geen carry omdat de sommatie 0+0+ carry van 1 = 1 is. Voor de rest van de kolommen is er geen sprake van dragen.
Het tellen van kolommen begint vanaf de rechterkant. Met 16-bits optelling kan er een overdracht plaatsvinden van de achtste kolom naar de negende kolom (naar links bewegend). De volgende tabel illustreert dit:

Rekenkundige en logische bewerkingen vinden plaats in de microprocessor op het moederbord van de computer.
Voor een 8-bits woordcomputer kan de carry niet automatisch van de achtste bit naar de negende bit gaan. Om dus twee 16-bits groepen in zo'n computer toe te voegen, moet de optelling twee keer gebeuren in paren van acht-acht bits. De carry wordt verplaatst en uitgevoerd door de software (programmering).
Om twee getallen op te tellen, kunnen de getallen eerst worden geconverteerd naar hun twee-complementvorm (zie hieronder) voordat ze worden opgeteld.
3.3 Het complement van twee en de aftrekking ervan van binaire getallen
Op het moederbord van de computer bevindt zich het geheugen en de microprocessor en andere circuits. Het geheugen bestaat uit een reeks cellen van acht bits. Voor een byte gaat elke bit een cel binnen. De microprocessor heeft een aantal geheugenlocaties. Deze locaties van het geheugentype worden registers genoemd. In de computer kunnen dus tijdelijk groepen bytes worden opgeslagen in het geheugen of in de registers van de microprocessor.
In elk van deze opslagplaatsen kan elke cel een 1 of een 0 bevatten, en niets anders. In het leven zijn er positieve en negatieve getallen. Een positief getal begint met een plusteken (+) en een negatief getal begint met een negatief teken (-). Wanneer het teken wordt weggelaten, wordt het getal als een positief getal beschouwd.
Om dit probleem van het aangeven van het teken van een getal in de computer op te lossen, worden de hele getallen in bereiken opgeslagen. Hele getallen zijn gehele getallen. Als er acht bits worden gebruikt om het bereik van mogelijke getallen op te slaan, wordt de meest linkse bit gebruikt als tekenbit. Als het getal begint met 0, is het getal een positief getal. Als het met 1 begint, is het getal een negatief getal. Als zestien bits worden gebruikt om het bereik van mogelijke getallen op te slaan, wordt de meest linkse bit gebruikt als tekenbit. Als het getal begint met 0, is het getal een positief getal. Als het met 1 begint, is het getal een negatief getal. De nummers in dit formulier worden ondertekende nummers genoemd.
In de praktijk kunnen er getallen met teken zijn voor 8 bits, 16 bits, 32 bits en 64 bits. Hoe groter het aantal bits dat wordt gebruikt, hoe groter het bereik aan mogelijke getallen dat kan worden opgeslagen.
Twee complementaire gehele getallen
Bij het twee-complement zijn de positieve getallen de normale telgetallen, behalve dat het meest linkse cijfer 0 is. Om het corresponderende negatieve getal voor een bepaald positief getal te verkrijgen, keert u elk bit van het getal om en telt u 1 op bij het resultaat. De omkering of aanvulling van 0 is 1. De omkering of aanvulling van 1 is 0. De volgende tabellen tonen de complementgetallen van enkele twee in hun bereik:
| Tabel 3.31 Twee complementaire gehele getallen in twee bits |
|
|---|---|
| Binair | Decimale |
| 01 | +1 |
| 00 | +0 |
| elf | -1 |
| 10 | -2 |
De positieve binaire getallen zijn 00 en 01 (dat is nul en één). In het meest linkse bit geeft nul aan dat het positieve getallen zijn. 00 ligt enigszins in het midden van het bereik. Om -1 te verkrijgen, blijkt de inversie van het getal 01 10 te zijn. Als je hier 1 aan toevoegt (uiterst rechts), krijg je 11.
Omdat er twee bits worden gebruikt, blijft er slechts één bit over om de getallen weer te geven in het bereik dat bestaat uit de getallen +1, +0 en -1 die overeenkomen met 01, 00 en 11. De eerste bit geeft het teken aan. Het komt voor dat 10 voor +2 niet tot deze drie binaire getallen behoort. 10 begint met 1, wat betekent dat het een negatief getal in het twee-complement moet zijn. Dus 10 is opgenomen in het bereik, wat betekent -2.
Met twee bits in twee-complement is het aantal van alle gehele getallen (positief en negatief) dat kan worden weergegeven 2 2 = 4 en niet 2 2 -1 = 3. De nuance is het resultaat van de opname van het laatste negatieve getal, dat het negatieve getal van 2 is nummermet – 1. In dit geval -2 2-1 = -2 1 = -2. Er is geen +2 in het bereik van twee-complementgetallen in 2 bits.
| Tabel 3.32 Twee complementaire gehele getallen in vier bits |
|
|---|---|
| Binair | Decimale |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
De positieve binaire getallen lopen van 0000 tot 0111 (dat wil zeggen van nul tot zeven). In het meest linkse bit geeft nul aan dat het positieve getallen zijn. 0000 ligt enigszins in het midden van het bereik. Om -1 te verkrijgen, blijkt de inversie van het getal 0001 1110 te zijn. Als je hier 1 aan toevoegt (uiterst rechts) krijg je 1111. Om -2 te verkrijgen, blijkt de inversie van 0010 1101 te zijn. Hieraan 1 toevoegen ( van uiterst rechts) geeft 1110. De andere negatieve binaire getallen zoals -3 tot -7 worden op dezelfde manier bepaald.
Omdat er vier bits worden gebruikt, blijven er drie bits over om de getallen in het bereik weer te geven: +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 en -7 overeenkomend met 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 en 1001.
De -8 die overeenkomt met 1000 moet afzonderlijk worden geadresseerd. Het eerste bit voor al deze getallen geeft het teken 0 aan voor positieve getallen en 1 voor negatieve getallen. Het komt voor dat 1000 niet tot deze veertien binaire getallen behoort. 1000 begint met 1, wat betekent dat het een negatief getal moet zijn, voor zover het het complement van twee betreft. Dus 1000 is opgenomen in het bereik, wat neerkomt op -8.
Met vier bits in twee-complement is het aantal van alle gehele getallen (positief en negatief) dat kan worden weergegeven 2 4 = 16 en niet 2 4 – 1 = 15. De nuance is het resultaat van de opname van het laatste negatieve getal, dat het negatieve getal van 2 is aantalBreedte – 1. In dit geval -2 4 -1 = -2 3 = -8. Er is geen +8 in het getallenbereik.
De eerdere analyse voor twee, vier en bredere bits in twee-complement kan worden toegepast op 8 bits, 16 bits, 32 bits en 64 bits brede binaire getallen.
Het twee-complement offert het eerste (meest linkse) bit op voor het teken 0 voor een positief getal en 1 voor een negatief getal. Voor de “n” bit brede groep bits zijn er 2 N totaal positieve plus negatieve getallen. Het zou 2 zijn N -1, ware het niet dat het gelukkige laatste (kleinste) negatieve getal erbij was inbegrepen. Het hoogste positieve getal is +2 n-1 -1 en het kleinste negatieve getal is -2 n-1 -1. Het zou -2 zijn n-1 -1, ware het niet dat de gelukkige -2 er was n-1 inbegrepen.
Getallen in twee-complement aftrekken
Bij aftrekken:
A – B = D
A wordt het minuend genoemd, B wordt de aftrekker genoemd en D wordt het verschil genoemd.
Om een positief binair getal af te trekken van een ander positief binair getal, wordt de minteken geschreven in twee-complement en wordt de aftrekker geconverteerd naar zijn negatieve twee-complementwaarde. De wiskundige verklaring wordt dus:
A+ – B = D
Met andere woorden: bij het aftrekken van twee complementen wordt het aftrekkertje omgezet in een negatief getal en vervolgens opgeteld bij het minteken.
Voorbeeld 3.31:
Evalueer de volgende decimale uitdrukking in twee-complement met behulp van vier bits:
6 – 4
Oplossing:
Het binaire getal voor 6 is 110. In 4-bits twee-complement is dit 0110. Het binaire getal voor +4 is 100. In 4-bits twee-complement is dit 0100. 0100 moet worden omgezet in negatief 4 in tweeën complementeer als volgt: Het complement of de inversie van 0100 is 1011. Als we hier vanaf de rechterkant 1 aan optellen, zoals we dat ook deden, krijgen we 1100. De decimale uitdrukking is dus:
6 – 4 wat wordt:
0110 – 0100 dus
0110 +(– 0100) = 0110 + 1100 gedaan zoals in de vorige optelsectie als:

Opmerking: 0110 +(– 0100) is hetzelfde als 6 + – 4
Bij het aftrekken van het twee-complement wordt elke carry, na de laatste kolom naar links, in de optelling weggegooid. Bij het aftrekken in decimalen is de wiskundige verklaring:
6 – 4 = 2
Als je hetzelfde doet in twee-complement, is het antwoord 0010, wat +2 is in twee-complement binair tellen. Bij de vorige aftrekking wordt een kleiner getal afgetrokken van een groter getal. In het volgende voorbeeld wordt een groter getal afgetrokken van een kleiner getal. Tabel 3.32 kan worden geraadpleegd om te zien of 0010 werkelijk het twee-complement is, wat equivalent is voor +2.
Voorbeeld 3.32:
Evalueer de volgende decimale uitdrukking in twee-complement met vier bits:
4 – 6
Oplossing:
Het binaire getal voor 4 is 100. In 4-bits twee-complement is dit 0100. Het binaire getal voor +6 is 110. In 4-bits twee-complement is dit 0110. 0110 moet worden omgezet in negatief 6 in twee-complement als volgt: Het complement of de inversie van 0110 is 1001. Als we hier vanaf de rechterkant 1 bij optellen, zoals we deden bij de vorige optelling, krijgen we 1010. De decimale uitdrukking is dus:
4 – 6 wat wordt:
0100 – 0110 dus
0100 +(– 0110) = 0100 + 1010 gedaan zoals in de vorige optelsectie als:

Opmerking: 4+ – 6 is hetzelfde als 0100 +(– 0110).
Bij het aftrekken van het twee-complement wordt elke carry, na de laatste kolom naar links, in de optelling weggegooid. Bij het aftrekken in decimalen is de wiskundige verklaring:
4 – 6 = -2
Als je hetzelfde doet in twee-complement, is het antwoord 1110, wat -2 is in twee-complement binair tellen. Tabel 3.32 kan worden geraadpleegd om te zien of 1110 werkelijk het twee-complement is, wat equivalent is voor -2.
3.4 Vermenigvuldiging van binaire getallen
In de verklaring:
A x B = P
A wordt de vermenigvuldiger genoemd, B wordt de vermenigvuldiger genoemd en P wordt het product genoemd. De uitdrukking A x B betekent dat A, B een aantal keren moet worden opgeteld wanneer A en B gehele getallen zijn (hele getallen).
Vermenigvuldiging in binair getal is hetzelfde als vermenigvuldiging in decimaal getal. In plaats van het decimaal te doen, wordt het echter binair gedaan. De vermenigvuldiging van de decimale uitdrukking van 42 x 10 gebeurt als volgt in binair getal, waarbij 42 10 = 101010 2 en 10 10 = 1010 2 :
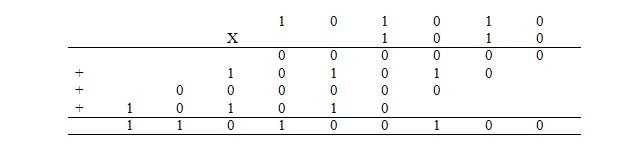
De 4 getallen die worden toegevoegd, worden deelproducten genoemd. Het antwoord is het product. Het toevoegen van de deelproducten gebeurt op dezelfde manier als eerder uitgelegd.
De vermenigvuldiging kan ook als volgt worden gezien: bij deze vermenigvuldiging met grondtal twee, als het bit (cijfer) in de vermenigvuldiger 1 is, is het minst significante bit van zijn gedeeltelijke product het minst significante bit van het vermenigvuldigingstal dat er direct onder opnieuw wordt getypt; en de rest van de bits van het vermenigvuldigtal worden naar links herhaald. Als bij deze vermenigvuldiging met grondtal twee het bit (cijfer) in de vermenigvuldiger 0 is, bestaat het gedeeltelijke product uit nullen met het minst significante bit van 0 er direct onder. Het aantal nullen is het aantal bits in het vermenigvuldigtal.
3.5 Verdeling van binaire getallen
In de verklaring:
EEN ÷ B = Q
A wordt het Dividend genoemd, B wordt de Deler genoemd en P wordt het Quotiënt genoemd. Het quotiënt kan vergezeld gaan van een rest. De uitdrukking A ÷ B betekent hoe vaak B kan worden opgeteld om A te geven of er dichtbij te komen, zodat de rest 0 of minder is dan B.
Verdelen kan op vele manieren. De hier afgebeelde indeling is de restauratieafdeling.
Herstel van verdeeldheid
Dit is de staartdelingsmethode die op scholen wordt geleerd. Als 237 wordt gedeeld door 6, is het antwoord 39 en rest 3. De 237 10 in basis 2 is 11101101 2 en 6 10 in grondtal 2 is 110 2 . De 39 10 in basis 2 is 100111 2 en 3 10 in basis 2 is 11 2 .
Dus 11101101 2 gedeeld door 110 2 geeft 100111 2 rest 11 2 in basis twee. Met de herstelmethode zijn de binaire getallen gewone getallen en zijn ze niet noodzakelijkerwijs in twee-complement. De volgende structuur verdeelt 11101101 2 door 110 2 om 100111 te geven 2 rest 11 2 :

Aftrekken gebeurt normaal gesproken en niet met behulp van het complement van de twee. Omdat dit basis twee is, is een lening twee en niet tien. De gedeeltelijke dividenden zijn 10, 101, 1011, 1010 en 1001. 11 is de rest. Omdat de deler drie cijfers heeft, gebeurt de deling in principe in groepen van drie cijfers vanaf het gegeven deeltal. Het quotiënt is het gehele getal (geheel getal) en voor dit probleem is dit 100111. Het quotiënt- en restresultaat is zoals verwacht.
3.6 Rekenkundige bewerkingen met software en hardware
Het moederbord van de computer heeft een klok. De tikken van de klok worden pulsen genoemd. Bij elke klokpuls worden op verschillende plekken op het moederbord één of meerdere beslissingen genomen; en dat heeft met programmeren (software) te maken.
Binnenin de microprocessor bevinden zich twee soorten circuits, genaamd: Combinational Logic Circuits en Sequential Logic Circuits. Er is een ander soort circuit dat een multiplexer wordt genoemd. Optellen, vermenigvuldigen en delen kan binnen één klokinterval plaatsvinden met behulp van de combinatorische logica (circuit). Terwijl programmeren (software) bij elke klokpuls een beslissing neemt met behulp van de sequentiële logische circuits en multiplexers.
Als er wordt afgetrokken met behulp van het twee-complement, zijn er minimaal twee klokpulsen nodig. Bij de eerste klokpuls kanaliseert een multiplexer de aftrekker naar een reeks NOT-poorten (één NOT-poort per cijfer). Bij de tweede klokpuls voegt de combinatorische logica 1 toe aan de uitvoer van de NOT-poorten en gaat door met het optellen van de resulterende aftrekker en minuend. Al dat optellen kan binnen één klokinterval plaatsvinden.
Optellen, vermenigvuldigen en delen kan nog steeds niet lukken met programmeren met behulp van de waarheidstabellen. Dit wordt echter niet behandeld in deze online carrièrecursus.
3.7 Logische bewerkingen in de microprocessor
AND, OR, XOR en Omkeren
EN
De volgende tabel illustreert de Bitwise AND. Dit betekent dat voor twee verschillende binaire getallen de overeenkomstige bits worden AND-gebaseerd op de AND Truth-tabel:
Van links naar rechts bewegend, 1 EN 1 = 1; 0 EN 1 = 0; 0 EN 0 = 0; 1 EN 0 = 0; enzovoort, in overeenstemming met de AND-waarheidstabel.
OF
De volgende tabel illustreert de Bitwise OR. Dit betekent dat voor twee verschillende binaire getallen de overeenkomstige bits worden ge-ORed op basis van de OR-waarheidstabel:

Van links naar rechts bewegend, 1 OF 1 = 1; 0 OF 1 = 1; 0 OF 0 = 0; 1 OF 0 = 1; enzovoort, in overeenstemming met de OR-waarheidstabel.
VRIJ
De volgende tabel illustreert de Bitwise exclusieve-OR. Dit betekent dat voor twee verschillende binaire getallen de overeenkomstige bits XORed worden op basis van de XOR Truth-tabel:

Van links naar rechts bewegend, 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1 XOR 0 = 1; enzovoort in overeenstemming met de XOR-waarheidstabel.
Omkeren (NIET)
De volgende tabel illustreert de Bitwise NOT (omkeren). Dit betekent dat voor één binair getal deze keer elke bit wordt omgekeerd op basis van de NOT Truth Table:

Van links naar rechts bewegend, NIET 1 = 0; NIET 0 = 1; NIET 0 = 1; NIET 1 = 0; enzovoort, in overeenstemming met de NIET-waarheidstabel.
Rechts of links verschuiven
Verschuiving naar rechts
Het volgende binaire getal wordt 3 bitposities naar rechts verschoven, waarbij de nullen in de vrijgekomen bitposities aan de linkerkant worden ingevoegd:

Het verschuiven kan voor één, twee, drie, vier, etc. plaatsen.
Verschuiving naar links
Het volgende binaire getal wordt 3 bitposities naar links verschoven, waarbij de nullen in de vrijgekomen bitposities aan de rechterkant worden ingevoegd:

Het verschuiven kan voor één, twee, drie, vier, etc. plaatsen.
Rechts of links draaiend
Roteren is vergelijkbaar met verschuiven. Het wordt stukje bij beetje gedaan. Bij het naar rechts draaien vallen de bits die het rechteruiteinde verlaten er niet af zoals bij het schakelen; ze vervangen de vrijgekomen bits aan de linkerkant één voor één. Bij het naar links draaien vallen de bits die het linkeruiteinde verlaten er niet af zoals bij het schakelen; ze vervangen de vrijgekomen bits aan de rechterkant één voor één.
Draai naar rechts
Het volgende binaire getal wordt 3 bitposities naar rechts gedraaid:

Het roteren kan voor één, twee, drie, vier, etc. plaatsen.
Roraat links
Het volgende binaire getal wordt 3 bitposities naar links gedraaid:

Het roteren kan voor één, twee, drie, vier, etc. plaatsen.
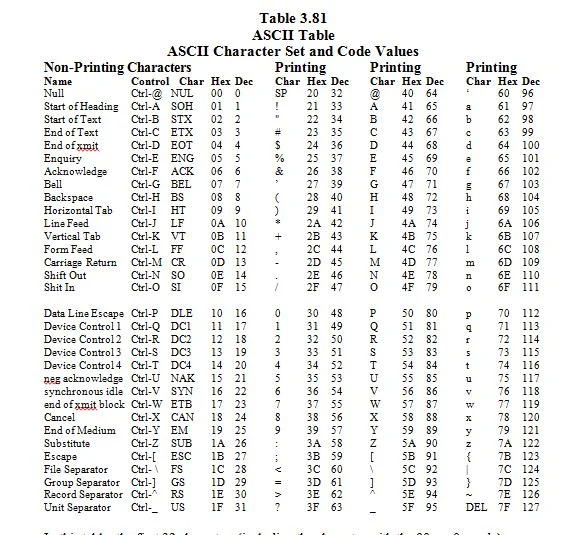
3.8 ASCII-tekenset en zijn codewaarden
ASCII staat voor “American (U.S.A) Standard Code for Information Interchange”. Stel je een toetsenbord voor met 96 toetsen. Dit is een ideaal toetsenbord waarbij de hoofdlettertoetsen anders zijn dan de kleine lettertoetsen. Elke andere toets vertegenwoordigt een teken dat voorkomt op een Engels (VS) toetsenbord. De tekens en codes (overeenkomende cijfers voor de tekens) worden hieronder vermeld:
In deze tabel worden de eerste 32 tekens (inclusief het teken met de 00 16 = 0 10 code) zijn niet-afdrukbare tekens. Het zijn controlekarakters. Ze zijn niet te zien op het scherm (monitor) waar alles gelijk is. Ze hebben alleen maar gevolgen. Laten we daar later meer over bespreken.
De rest van de karakters zijn gedrukte karakters; ze zijn te zien op het scherm. Er zijn 128 ASCII-tekens. 2 7 = 128. 1.111.111 2 = 127 10 . De 7 in 2 7 betekent 7 bits.
Nu, 1111111 2 + 1 2 is hetzelfde als:
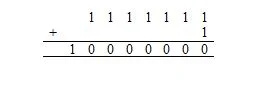
Hier 10.000.000 2 = 128 10 . Er zijn 128 10 tekens in de vorige lijst (tabel) met ASCII-tekens. Dit omvat het nulteken, waarvan de code in grondtal zestien (hexadecimaal) 00 is, wat overeenkomt met 0 in grondtal tien.
Aangezien er in totaal 128 tekens zijn, levert 128 min 32 niet-afdrukbare tekens 96 afdruktekens op. In deze sectie wordt aangenomen dat er een ideaal toetsenbord bestaat met 96 tekens die afdrukbaar zijn. Op dit ideale toetsenbord zijn de toetsen voor Engelse hoofdletters anders dan de toetsen voor Engelse kleine letters.
Elk teken op het toetsenbord wordt weergegeven door een grondgetal van 7 bits, dat niet in de lijst wordt weergegeven. De hoofdletter van “N” wordt bijvoorbeeld weergegeven door de zeven bits 1001110 in basis 2. Om 1001110 te converteren 2 naar grondtal 16, laat het voorafgaan door 0 en groepeer het resultaat als volgt in subgroepen van vier bits:
| 0100 | 1110 | 2 = | 4 | E | 16
Dat is 01001110 2 = 4E 16 . Om 4E om te zetten 16 naar grondtal tien, doe het volgende:
4 x (16) 1 + V x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
Rechts van “N” in de lijst (tabel) staat het hexadecimale getal van 4E en het decimale getal van 78.
Nog een voorbeeld: het teken “[“ wordt weergegeven door de zeven bits 1011011 in grondtal 2. Om 1011011 te converteren 2 naar grondtal 16, laat het voorafgaan door 0 en groepeer het resultaat als volgt in subgroepen van vier bits:
| 0101 | 1011 | 2 = | 5 | B | 16
Dat is 01011011 2 = 5B 16 . Ga als volgt te werk om 5B16 naar grondtal tien te converteren:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
Rechts van “[“ in de lijst (tabel) staat het hexadecimale getal 5B en het decimale getal 91.
Als nog een ander voorbeeld wordt het teken voor het decimale getal “5” weergegeven door de zeven bits 0110101 in basis 2, en niet 0000101 in basis 2. Om 0110101 om te zetten 2 naar grondtal 16, voorafgegaan door 0 en groepeer het resultaat als volgt in subgroepen van vier bits:
| 0011 | 0101 | 2 = | 5 | B | 16
Dat is 00110101 2 = 35 16 . Ga als volgt te werk om 3516 naar grondtal tien te converteren:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
Rechts van “5” in de lijst (tabel) staat het hexadecimale getal van 35 en het decimale getal van 53.
Omdat de computer in bytes werkt, worden er bij het indrukken van een toets op het ideale toetsenbord acht bits naar de microprocessor (moederbord) gestuurd. Het ideale toetsenbord is een randapparaat dat gescheiden is van de systeem(basis)eenheid van de computer. Het heeft een elektronisch circuit (IC) dat de zeven bits creëert en voorafgaat door een nul voordat het via de kabel naar het moederbord van de systeemeenheid wordt gestuurd. Vanaf de ingangspoort (ingangscircuit) van het moederbord gaat het naar de microprocessor die zich ook op het moederbord bevindt. Vanuit de microprocessor gaat het naar het geheugen dat ook op het moederbord zit.
Wanneer dus de “N”-toets op het ideale toetsenbord wordt ingedrukt, worden acht bits 01001110 naar de microprocessor gestuurd. Vanuit de microprocessor worden ze naar het geheugen gebracht waar ze als byte op een geheugenlocatie blijven staan. De computerprogrammeur moet er rekening mee houden dat de acht bits van 01001110 2 is hetzelfde als 4E 16 dat is hetzelfde als 78 10 .
Wanneer de “[“-toets op het ideale toetsenbord wordt ingedrukt, worden acht bits 01011011 naar de microprocessor gebracht. Vanuit de microprocessor worden ze naar het geheugen gebracht waar ze als byte op een geheugenlocatie blijven staan. De computerprogrammeur moet er rekening mee houden dat de acht bits van 01011011 2 is hetzelfde als 5B 16 dat is hetzelfde als 91 10 .
Wanneer de “5”-toets op het ideale toetsenbord wordt ingedrukt, worden als teken en niet als decimaal getal acht bits 00110101 naar de microprocessor gebracht. Vanuit de microprocessor worden ze naar het geheugen gebracht waar ze als byte op een geheugenlocatie blijven staan. De computerprogrammeur moet er rekening mee houden dat de acht bits van 00110101 2 is hetzelfde als 35 16 dat is hetzelfde als 5310 10 .
Er zijn momenten waarop een programma draait en wacht tot het decimale getal 5 in de computer is ingevoerd. Als in deze situatie de “5”-toets op het ideale toetsenbord wordt ingedrukt, wordt nog steeds de acht-bits code 00110101 naar de microprocessor gestuurd. Omdat wat nodig is het decimale getal 5 is, en niet het teken “5”, gebruikt een stukje code (kort programma) uit het geheugen de microprocessor om de tekencode 00110101 in grondtal twee om te zetten naar het twee-complementnummer 00000101 2 voordat het naar een geheugenlocatie wordt verzonden als een twee-complementbyte. De computerprogrammeur moet er rekening mee houden dat 00000101 5 betekent 10 in basis 2, en verschilt van de codenummers van 00110101 2 , 35 16 en 53 10 wat het karakter van “5” betekent. Om het twee-complementnummer 00000101 in het geheugen weer te geven, moet een ander kort programma 00000101 uit het geheugen omzetten naar 00110101. Het is 00110101, wat hetzelfde is als 35 16 dat is hetzelfde als 53 10 dat op de monitor wordt weergegeven (of door de printer op papier wordt afgedrukt).
3.9 Getalnotatie met drijvende komma
Een getal zonder decimaal deel is een geheel getal. Het getal 36 is een geheel getal. 36,375 is geen geheel getal. Het is een decimaal getal met een decimaal gedeelte. Het decimale deel van .375 is een breuk die kleiner is dan 1.
36,375 wordt in decimale vorm geïnterpreteerd als:
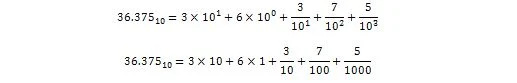
Nu:
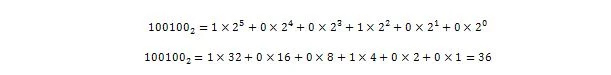
Dus 100100 2 = 3610, wat het gehele getal is van 36,375 10 .
Nu:
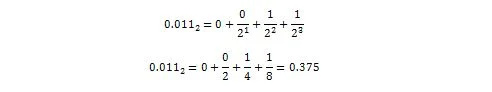
Dus 0,011 2 = 0,375 10 dat is het decimale getalgedeelte van 36,375 10 .
∴ 36.375 10 = 100100,011 2
Anders gezegd:
100100.011 2 = 36.375 10
Getallen worden in de computer weergegeven in grondtal 2 en niet in grondtal 10, waarbij alles gelijk is. Omdat een cel in een register in de microprocessor of een cel in het geheugen slechts 1 of 0 kan bevatten, is er geen ruimte om een decimaalpunt op te slaan. Dit vormt een probleem. Als resolutie is er de IEEE-754 32-bits drijvende-kommaweergave met enkele precisie en de IEEE-754 64-bits drijvende-kommaweergave met dubbele precisie.
32-bits getalnotatie met drijvende komma
Het getal 100100.0112 kan worden uitgedrukt als:
100100.011 2 = 1,00100011 2 x 2 +5
De rechterkant van het =-symbool wordt in de wiskunde de standaardvorm van basis twee van de linkerkant van 100100.011 genoemd 2 .
Nu 00100011 van 1.00100011 2 aan de rechterkant van het =-symbool, zonder de voorafgaande “1.” en zonder de 2 voor het grondtal wordt dit de expliciete significantie genoemd. In dit geval wordt het binaire punt vijf plaatsen naar links verplaatst om de “1” te verkrijgen. Verwar de komma en de binaire komma niet. Binaire punt is voor grondtal 2, terwijl decimale punt voor grondtal 10 is. De “1.” gevolgd door 00100011 aan de rechterkant van het =-symbool, zonder de 2 voor de basis, vormt de ware significantie. 1,00100011 wordt echter de impliciete significantie genoemd.
Na de significantie aan de rechterkant staat de “x 2 +5 ' uitdrukking. Met deze uitdrukking wordt de +5 de exponent genoemd. Het plusteken betekent dat het binaire punt vijf plaatsen naar voren moet worden verplaatst om op de normale oorspronkelijke positie te komen en dat 2 de basis is voor de nummering. De vorige vergelijking kan omgekeerd worden geschreven als:
1.00100011 2 x 2 +5 = 100100,011 2
Bij de 32-bits drijvende-kommaweergave is dit “1.00100011 2 x 2 +5 ” dat wordt gebruikt en niet alleen “100100.011 2 ”. De 2 voor de basis wordt niet geregistreerd. De 32-bit drijvende-kommaweergave voor het bestand “1.00100011 2 x 2 +5 ”-nummer, wat gelijk is aan 36.375 10 = 100100,011 2 , wordt weergegeven in de volgende tabel:

Er zijn 32-bits posities die vanaf het rechteruiteinde zijn genummerd, beginnend bij 0. Het eerste bit aan het linkeruiteinde is het tekenbit. Als het getal positief is, is dit bit 0. Als het getal negatief is, is dit bit 1 (-1 bestaat uit twee tekens en kan niet in één cel worden geplaatst). De 1.00100011 2 x 2 +5 wat gelijk is aan 36,375 10 wat ook gelijk is aan 100100.011 2 is een positief getal. Het eerste bit is dus 0.
Er zijn acht bitposities voor de exponent, beginnend vanaf positie 30 tot en met positie 23. De exponent die daar staat is echter 10000100 2 wat gelijk is aan 132 10 . De exponent van het getal van belang is eigenlijk +5 van het grondtal van twee. Dus, wat gebeurt er?
Nu wordt in het 32-bits formaat een exponent van 0 geschreven als 01111111 2 wat gelijk is aan 127 10 . De +5 10 +101 2 . Dus om uit te komen op 10000100 2 in het exponentgedeelte in de tabel, 101 2 werd toegevoegd aan 01111111 2 , dienovereenkomstig. Het betekent dat 5 werd toegevoegd aan 127 om 132 te hebben 10 .
De significante, zonder “1.”, bracht de posities 22 terug naar 15, inclusief. Merk op dat de 1 van “1.” is niet aangegeven in de 32-bits string. Het wordt nooit aangegeven – accepteer dat. De rest van de cellen tot positie 0 zijn gevuld met nullen.
Als de werkelijke exponent -5 is, wordt 5 afgetrokken van 127 10 122 hebben 10 . Dit komt overeen met het aftrekken van 101 2 vanaf 01111111 2 om 01111010 te hebben 2 .
Bij alle voorgaande illustraties is het getal +1 gelijk aan 1,0 x 2 0 = 1,0 x 1 = 1,0 wordt weergegeven als:

Merk op dat de “1.” van 1,0 x 2 0 staat niet vermeld in het formaat. Het is nooit aangegeven. De volgende gemengde breuk die positief wordt na 1,0 is:

Let op de 1 aan het rechteruiteinde. Deze weergave is het nummer:

Het verschil tussen 1,0000001192092896 en 1,0 is:
1,0000001192092896 – 1,0 = 0,0000001192092896
De getallen met decimale delen zijn gemengde breuken. Niet alle breuken tussen 1 10 en 2 10 kan op de computer worden weergegeven. Er kan worden aangenomen dat de kleinste fractionele kloof tussen de opeenvolgende gemengde getallen met het 32-bit drijvende-kommaformaat 0,0000001192092896 is. Verwacht dat het interval voor dubbele precisie kleiner is. Raadpleeg de volgende afbeelding.
Als representatie van het getal volgt 0,0 niet de voorgaande argumenten. De representatie voor 0,0 wordt gedeclareerd en moet als zodanig worden geleerd. Om 0,0 weer te geven, zijn alle cellen voor de significantie 0 en zijn alle cellen voor de exponent ook nul. Het tekenbit kan 0 of 1 zijn. Helaas leidt dit als volgt tot positieve 0 en negatieve 0:

In het echte leven is er maar één nul. Positieve 0 en negatieve 0 bestaan niet. 0 wordt echter meestal als positief beschouwd. Positieve 0 en negatieve 0 bestaan hier vanwege deze specifieke formaatbeschrijving. De getallenlijn (zie hierboven) kan ook +0 en -0 hebben, maar er bestaat slechts één nul.
64-bits getalnotatie met drijvende komma
Het 64-bits drijvende-kommaformaat is vergelijkbaar met het 32-bits formaat, maar met de volgende verschillen:
- Er zijn 64 bits om een getal weer te geven.
- Na het tekenbit zijn er 11 bits voor het exponentnummer.
- Het exponentnummer voor de nulindex (2 0 ) is 1023 10 = 01111111111 2 .
- De elf bits worden gevolgd door 52 bits voor de expliciete significantie.
- Het heeft een breder bereik aan getallen dan het 32-bits formaat.
Merk op dat de “1.” dat wil zeggen aan het begin van de significantie is nog steeds niet opgenomen in de 64 bits, net zoals het niet is opgenomen in de 32 bits voor het 32-bits formaat.
Een van de belangrijkste verschillen tussen het 64-bits formaat en het 32-bits formaat is dat het verschil tussen de opeenvolgende gemengde fracties in het 64-bits formaat kleiner is dan dat van het 32-bits formaat.
In het 64-bits formaat kan het interval (gat) tussen 1,0 en de volgende gemengde fractie als volgt worden berekend:
1,0 wel
0 01111111111 00000000000000000000 00000000000 000000000000000000000 2
Dit komt overeen met de “1.”, die niet in de string is aangegeven, vermenigvuldigd met 2 tot de macht (index) 0 (waarbij de exponent 1023 is). 10 = 01111111111 2 voor 2 0 = 1). De tekenreeks is 1,0 x 2 0 .
De volgende gemengde fractie groter dan 1,0 is:
0 01111111111 00000000000000000000 00000000000 000000000000000000001 2
Dit komt overeen met “1.” die niet in de string wordt aangegeven, gevolgd door 51 nullen, en dan 1, vermenigvuldigd met 2 tot de macht 0 (waarbij de exponent 1023 is 10 = 011111111112 2 voor 2 0 = 1). Dit is hetzelfde als:
+2 0 × (1 + 2− -52 ) ≈ 1,0000000000000002
De ≈ betekent ongeveer gelijk aan.
Nu:
1,0000000000000002 – 1,0 ≈ 0,0000000000000002
De corresponderende intervalwaarde voor een 32-bits formaat is 0,0000001192092896 ≈ 0,00000012.
0,0000000000000002 is veel kleiner dan 0,00000012. Er zijn dus veel meer gemengde breuken tussen twee opeenvolgende gehele getallen (bijvoorbeeld 3 en 4) in het 64-bits formaat dan tussen twee opeenvolgende gehele getallen voor het 32-bits formaat.
Het aantal gemengde breuken tussen twee opeenvolgende gehele getallen op de getallenlijn is oneindig. Geen enkel formaat (bijvoorbeeld 32-bits of 64-bits) kan dus alle gemengde breuken tussen twee opeenvolgende gehele getallen (hele getallen) opleveren. Hoe kleiner de opening (interval) tussen twee opeenvolgende gehele getallen die door een formaat worden geboden (bijvoorbeeld 32-bits of 64-bits), hoe groter het aantal gemengde breuken tussen de opeenvolgende gehele getallen (voor de getallenlijn).
De redenen waarom het 64-bits formaat wordt beschreven als dubbele of hogere precisie, vergeleken met het 32-bits formaat, zijn dat het interval tussen twee opeenvolgende gemengde breuken begrensd door twee opeenvolgende gehele getallen voor het 64-bits formaat kleiner is dan de overeenkomstige 32 bits. -bit formaatinterval. Ook zijn er meer gemengde breuken mogelijk tussen twee begrensde gehele getallen voor het 64-bits formaat dan dienovereenkomstig voor het 32-bits formaat.
Een decimaal deel (fractie) van een decimaal getal omzetten in een binair deel
De 36,375 is een decimaal getal met het decimale deel “.375”. Het decimale deel van “.375” is een breuk tussen nul en één. De 0,5 in basis tien heeft dezelfde waarde als 1/2 in basis twee. De 0,5 10 die wordt uitgedrukt met de basis twee-uitbreiding is:
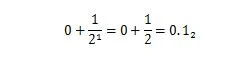
Het is niet 0,101 2 wat 0,625 betekent 10 . Het decimale deel van een decimaal getal heeft zijn equivalente binaire deel voor het overeenkomstige binaire getal. Dus om een decimaal getal zoals 36,375 om te zetten 10 om grondtal twee te bepalen, converteer je 36 naar binair en converteer je vervolgens .375 ook naar binair. Voeg vervolgens beide resultaten samen met het binaire punt. De methoden om de twee secties te converteren zijn verschillend. Hoe je een decimaal geheel getal naar grondtal 2 converteert, wordt uitgelegd in hoofdstuk 1.
Volg de volgende stappen om de decimale breuk naar een binaire breuk te converteren:
- Vermenigvuldig de decimale breuk (decimaal deel) met 2. Het gehele getal dat hieruit voortkomt is het eerste binaire cijfer.
- Herhaal de vorige stap met het fractionele decimale resultaat om het volgende binaire cijfer te krijgen.
- Blijf de vorige stap herhalen totdat het decimale breukresultaat .0000 is.
Voorbeeld: Converteer het fractionele deel van 36,375 10 naar het equivalente fractionele deel in basis twee.
Oplossing:
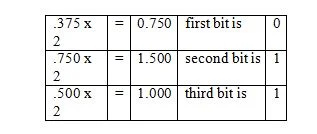
Merk op dat in de derde stap .500 werd vermenigvuldigd met 2 en niet de 1.500. De binaire overeenkomstige breuk wordt in de laatste kolom van boven afgelezen. En dus is het volgende resultaat:
.375 10 = .011 2
Een binair deel (fractie) van een binair getal omzetten in een decimaal deel
Om dit te bereiken, breidt u de binaire breuk uit in wederkerige machten van 2.
Voorbeeld: Converteer het fractionele deel van 100100,011 2 naar het equivalente fractionele deel in basis tien.
Oplossing:
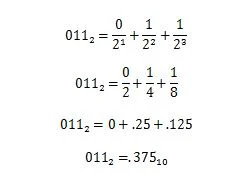
3.10 Nummervoorvoegsels in computers
In het normale leven betekent 1 kilo 1000, wat wordt afgekort in k (kleine letters) zoals in 1kg. In de computerwereld betekent 1 kilo 2 10 = 1024, maar wordt afgekort in K (hoofdletters) zoals in 1Kbits. In het normale leven betekent 1 mega 1.000.000, wat wordt afgekort in M (hoofdletters) zoals in 1Mg. In de computerwereld betekent 1 mega 2 twintig = 1.048.576 = 2 10 x 2 10 = 1024 x 1024 = 1.048.576 en wordt nog steeds afgekort in M (hoofdletters) als in 1Mbits. In het normale leven betekent 1 giga dat 1.000.000.000 wordt afgekort in G (hoofdletters) zoals in 1Gg. In de computerwereld betekent 1 giga 2 30 = 1.073.741.824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1.073.741.824 en wordt nog steeds afgekort in G (hoofdletters) als in 1Gbits. De volgende tabel geeft de betekenis van vier voorvoegsels in het normale leven en in de computerwereld:
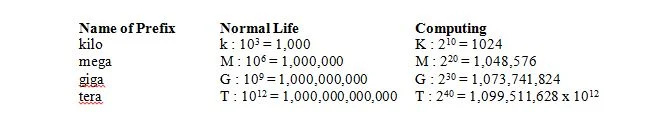
3.11 Problemen
De lezer wordt geadviseerd alle problemen in een hoofdstuk op te lossen voordat hij naar het volgende hoofdstuk gaat.
- Teken een getallenlijn met gehele getallen van -10 tot +10.
- Voeg de volgende binaire getallen toe in 8-bits twee-complement: 101010 2 en 1111 2 .
- Gebruik alleen de twee-complementbenadering in 8-bits om het binaire getal 1111 af te trekken 2 van het binaire getal 101010 2 .
- Zoek het product van 10110 2 x 1101 2 in basis twee.
- Verdeel 36.375 10 tegen 1000 10 in decimaal en binair, en vergelijk de resultaten.
- Gebruik de 8-bits van uw keuze om de logische AND, OR, XOR, Invert, Shift Right, Shift Left, Rotate Right en Rotate Left te illustreren. Elke byte moet een combinatie van 1-en en 0-en bevatten.
- a) Schrijf de numerieke code voor het ASCII-teken nul in hexadecimaal, binair en decimaal.
b) Schrijf de numerieke code voor het ASCII-teken “1” in hexadecimaal, binair en decimaal.
c) Schrijf de numerieke code voor het ASCII-teken “A” in hexadecimaal, binair en decimaal.
d) Schrijf de numerieke code voor het ASCII-teken “a” in hexadecimaal, binair en decimaal. - Converteren 49,49 10 in basis twee. Converteer uw resultaat naar het IEEE 32-bit drijvende-kommaformaat.
- a) Waarin verschilt het IEEE 64-bits drijvende-kommaformaat van het 32-bits formaat?
b) Geef de twee gerelateerde redenen waarom het 64-bits formaat wordt beschreven als een dubbele of hogere precisie dan de
32-bits formaat.